Random measurement errors associated with short-term dietary assessment instruments (e.g., 24-hour dietary recalls and food records) may cause unexpected bias depending on study objective and target statistic. Fortunately, there are well established methods to mitigate the impact of random errors. One of these methods is called regression calibration. In this blog, I introduce the method and show how it can be applied to a simple nutrition analysis.

What is ‘regression calibration’ ?

Regression calibration is one of the statistical methods available to correct the bias due to random errors. The method traditionally requires one or many repeated measurements (Kirkpatrick et al. 2022). The method consists of the regression of a repeat measurement on the first measurement using a linear regression model (measurement error model). This measurement error model allows to obtain a correction factor which can then be used to calibrate the association of interest.

Regression calibration was first used to obtain unbiased regression coefficient estimate in a linear regression of a continuous outcome on a covariate measured with error, but the method also works well for logistic or Cox regression models (Keogh et al. 2020).

I want to point out that comprehensive methods have been developed for nutrition analyses, including the National Cancer Institute (NCI) methods. Example applications for the National Cancer Institute methods are available at Software for Measurement Error in Nutrition Research. The NCI methods also cover a wide range of application and are not limited to regression models. Informally, the NCI methods are very fancy and powerful applications of regression calibration designed for a variety of analysis.

Requirements and assumptions

The regression calibration method has statistical assumptions and requirements. In the list below, $i$ refers to a given individual and $j$ refers to a given short-term measurement of dietary intakes (e.g., a 24-h dietary recall or food records). Regression calibration:

1. Requires at least 50 repeated measurements over non-consecutive days ($n_{i,j=2}\ge 50$; Kirkpatrick et al. 2022 for details);
2. Requires satisfying the classical measurement error model assumptions:
   1. Random errors are normally distributed $E_{j} \sim N(\mu=0,\sigma_{\epsilon}^{2})$;
   2. Random errors across repeat measurements are independent (non-consecutive days) $E_{j=1} \perp E_{j=2}$;
   3. Random errors are independent of covariates included, if any $E_{ij} \perp Z_{i}$;
3. The random errors structure (i.e., the variation of intakes from one day to another) is generalizable to the full sample or specific subgroup (e.g., by sex);

Applying a measurement error correction method also requires us to assume that the self-reported dietary intakes are unbiased. In other words, that self-reported dietary intakes measured with the short-term dietary assessment instrument are the true intakes (Kirkpatrick et al. 2022). We know this assumption is not exactly correct (people tend to underreport their intakes), but it is a working assumption.

Example application: one independent variable measured with error

A common study objective is to estimate the relationship between a dietary factor, as independent variable, and an outcome, as dependent variable. For a continuous outcome, the estimand is $E(Y|X)$ or the expected value of $Y$ given $X$. For such analysis, we could be interested in the relationship between intake of vegetables and fruits (servings/day) and low-density lipoproteins (LDL) cholesterol concentrations as outcome; an association was found previously (Djousse et al. 2004). For this example, we will estimate the expected LDL cholesterol concentrations based on the intake of vegetables and fruits in a sample of the population ($n=5000$).

We could measure vegetables and fruits intake with 24-h dietary recall data since this instrument has minimal systematic error (Thompson et al. 2015). Knowing that 24-hour dietary recalls are affected by random errors, we collect a second 24-hour dietary recall to apply correction methods. Of note, to isolate the impact of random errors, I assume that LDL cholesterol concentrations are measured perfectly and that there is no source of bias (no confounding, no selection bias, no differential errors,…).

To assess the relationship between vegetables and fruits and LDL cholesterol, we would use a linear regression model corresponding to $Y_i=\beta_0 + \beta_{X_i} X_i +\epsilon_i$. However, a naive analysis ignoring random errors would rather have the estimand $E(Y|W_j)$ and model equation $Y_i=\beta\prime_0 + \beta\prime_{W_i} W_i +\epsilon_i$ .

Generate data

In this simulation, each increase of 1 serving of vegetables and fruits will decrease LDL cholesterol concentrations by 0.10 mmol/L. -10 mmol/L is the true regression coefficient $\beta_{X}$ for this association.

# ********************************************** #
#           Prepare simulated measures           #
# ********************************************** #

set.seed(1)

# generate the 'true' value (no random errors)
  X  <- rnorm(n=5000, mean=5, sd=1)
  
# generate independent random errors
  E1 <- rnorm(n=5000, mean=0, sd=1.3)
  ## change seed that have different values of random error
  set.seed(2)
  E2 <- rnorm(n=5000, mean=0, sd=1.3)
  
# Add random errors to the 'true' value to derive X measured "on a given day"
  W1 <- X+E1
  W2 <- X+E2
  
    ## For plausibility, truncate negative
    ## values at 0 (i.e., cant have negative intakes)
    W1 <- ifelse(W1<0,0,W1)
    W2 <- ifelse(W2<0,0,W2)
    
# generate a linear relationship based on X
  b0 <- 3.0 # hypothetical average LDL cholesterol in this sample
  b1 <- -0.10 # hypothetical relationship between vegetables and fruits and cholesterol
  EQ <-  b0 + b1 * X
  Y  <-  rnorm(n=5000, EQ, sd=0.5)

The proportion of total variance due to random errors for vegetables and fruits intakes is approximately 62% for $W_1$ and 61% for $W_2$. This is consistent with dietary intake data on a given day where a majority of the total variance is simply due to within-individual variations from one day to another (i.e., random errors). In other words, the majority of the variance for dietary intakes measured on a given day is caused by people eating a bit differently each day for random reasons.

Assess relationship using a linear regression model

First, I assess the relationship based on the naive analysis which considers the measured vegetables and fruits on a given day as if it reflects long-term/usual intakes. Then, I repeat the analysis with the true value, i.e., vegetables and fruits intake measured without errors that correctly reflect long-term/usual intakes.

Typically, we would not know the true vegetables and fruits intakes. This would require observing the actual intakes of many individuals over may days or months! Plus, had we known the true intakes, we would not need to apply measurement error correction as there would be no errors to correct.

# ********************************************** #
#        Association for naive analysis          #
# ********************************************** #

# Model for E(Y|W)
naive <- lm(Y ~ W1)

## Output model parameters
  library(parameters)
  naive_param <- 
    parameters::model_parameters(naive)

naive_param

Parameter   | Coefficient |       SE |         95% CI | t(4998) |      p
------------------------------------------------------------------------
(Intercept) |        2.69 |     0.02 | [ 2.65,  2.74] |  117.43 | < .001
W1          |       -0.04 | 4.36e-03 | [-0.05, -0.03] |   -9.16 | < .001

# ********************************************** #
#                True association                #
# ********************************************** #

# Model for E(Y|X)
true <- lm(Y ~ X)

## Output model parameters
true_param <- 
  parameters::model_parameters(true)

true_param

Parameter   | Coefficient |       SE |         95% CI | t(4998) |      p
------------------------------------------------------------------------
(Intercept) |        3.05 |     0.04 | [ 2.98,  3.12] |   86.81 | < .001
X           |       -0.11 | 6.89e-03 | [-0.13, -0.10] |  -16.24 | < .001

Regression coefficient of $\beta\prime_{W_j}$ vs. true association

The naive analysis indicates that a 1-serving increase in vegetables and fruits is associated with a 0.04 mmol/L lower LDL cholesterol concentrations (95%CI, -0.05, -0.03). However, the analysis based on true intakes rather indicates that a 1-serving increase in vegetables and fruits is associated with a 0.11 mmol/L lower LDL cholesterol concentrations (95%CI, -0.13, -0.10), which is consistent with the simulated association. The naive analysis shows a 2.8-fold attenuation of the true relationship. This observation is consistent with theory regarding the impact of one independent variable measured with (classical) random errors on an estimated regression coefficient (Keogh et al. 2020).

Standard error of $\beta\prime_{W_j}$ vs. true association

A noteworthy observation is that the standard error of the naive analysis is 1.6-fold smaller than the standard error of the true simulated association. Consequently, the estimated confidence interval for the naive analysis is narrower than the confidence interval of the true simulated association. The naive association not only underestimates the true association effect size, but it also produces an incorrectly narrow (and falsely precise) confidence interval.

Measurement error correction with regression calibration

Descriptive statistics and overview

It is good practice to look at the raw data before further analyses.

# ********************************************** #
#      Combine measured values with outcome      #
# ********************************************** #

# Create data with only measured vegetables and fruits (VF) and outcome
VF_simstudy <- 
  data.frame(
  VF_day1 = W1,
  VF_day2 = W2,
  LDL_cholesterol = Y)

# show 5 first rows
head(VF_simstudy)

   VF_day1  VF_day2 LDL_cholesterol
1 2.402261 3.207557        1.697239
2 6.001527 5.423947        2.232436
3 1.982719 6.228570        2.406524
4 8.128996 5.125792        2.507730
5 6.782459 5.225180        2.216356
6 2.570475 4.351678        2.046728

# ********************************************** #
#             Descriptive statistics             #
# ********************************************** #

# Intake on first assessment (on a given day)
## mean intakes
mean(VF_simstudy$VF_day1)

[1] 4.985152

## range (min to max)
range(VF_simstudy$VF_day1)

[1]  0.00000 10.93836

## histogram
hist(VF_simstudy$VF_day1)

# Intake on second assessment (on a given day, non-consecutive)
## mean intakes
mean(VF_simstudy$VF_day2)

[1] 5.048887

## range (min to max value)
range(VF_simstudy$VF_day2)

[1]  0.00000 11.01431

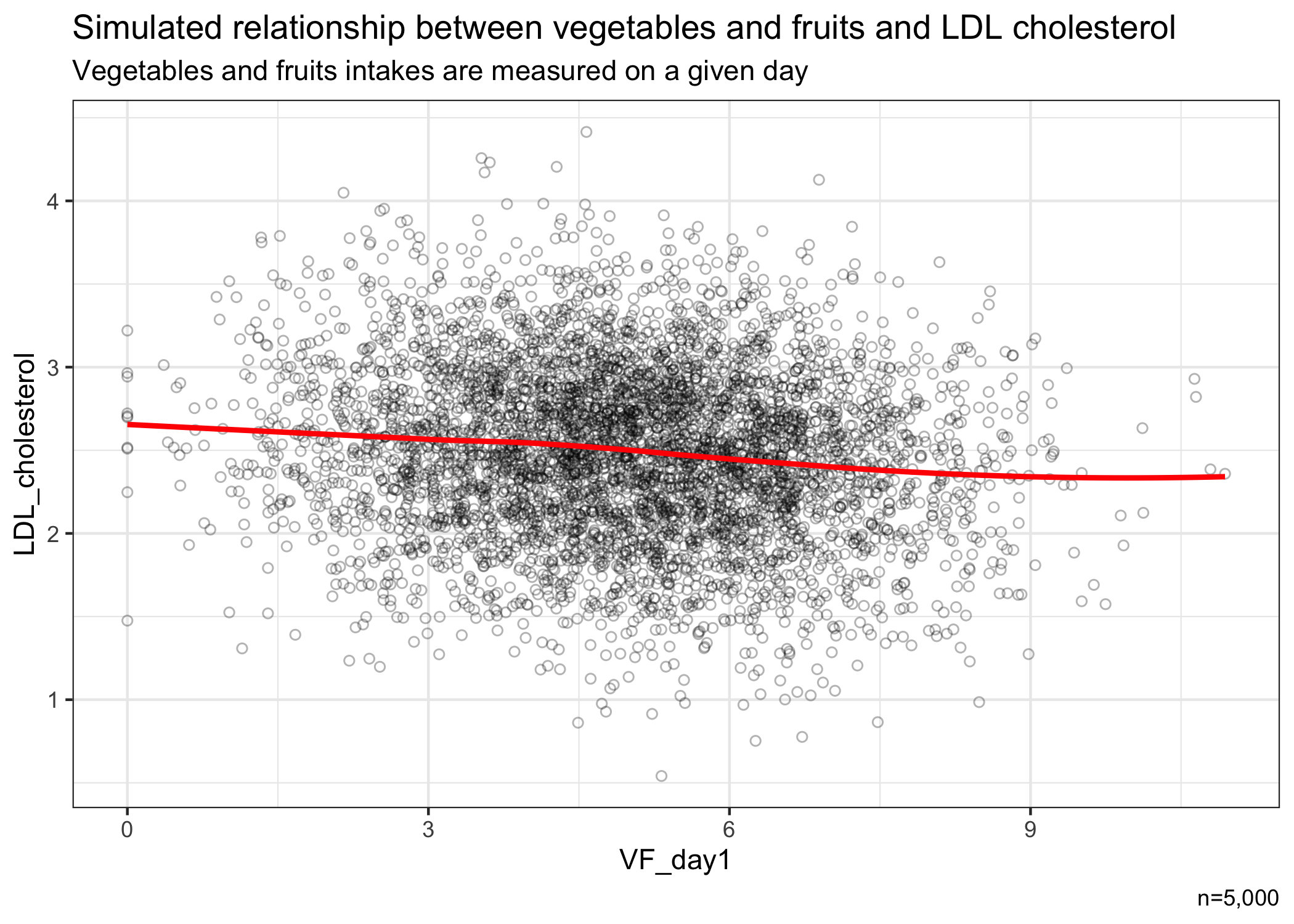
# show relationship 
library(ggplot2)

ggplot(data=VF_simstudy,aes(x=VF_day1,y=LDL_cholesterol)) +
  geom_point(alpha=0.3,shape=1) +
  geom_smooth(method="loess",se=FALSE,color="red") + 
  labs(title="Simulated relationship between vegetables and fruits and LDL cholesterol",
       subtitle="Vegetables and fruits intakes are measured on a given day",
       caption="n=5,000") +
  theme_bw()

Hand calculation

For the present demonstration of one independent variable measured with error (vegetables and fruits) in a linear regression model, the biased regression coefficient of the naive analysis can be calibrated directly using the following equation (Keogh and White, 2020):

which reads as: the unbiased (calibrated) regression coefficient of the association between vegetables and fruits and LDL cholesterol $\beta_X$ equals to the biased (naive) regression coefficient obtained with measured vegetables and fruits on a given day $\beta\prime_{W_J}$ divided by the correction factor $\lambda$.

The question is then, how can we estimate the correction factor $\lambda$? This is the purpose of regression calibration. As shown in Keogh and White (2020), we can estimate the correction factor $\lambda$ by the regression of the replicate measurement $W_{j=2}$ on the first measurement $W_{j=1}$. The equation is:

For the present demonstration, there are no covariates $Z_i$ and the equation simplifies to $W_{i,j=2} = \beta_0 + \boldsymbol{\lambda} W_{i,j=1} +\epsilon_i$.

# ********************************************** #
#     Hand calculation of correction factor      #
# ********************************************** #

# Regression of the second measurement (repeat) on first measurement
rc <- 
  glm(formula = VF_day2 ~ VF_day1, # had we considered covariates, we should have included them
      family  = gaussian("identity"),
      data    = VF_simstudy)

  ## Show parameters
  parameters::model_parameters(rc)

Parameter   | Coefficient |   SE |       95% CI | t(4998) |      p
------------------------------------------------------------------
(Intercept) |        3.09 | 0.07 | [2.96, 3.23] |   44.71 | < .001
VF day1     |        0.39 | 0.01 | [0.37, 0.42] |   29.74 | < .001

  ## Output correction factor (lambda)
  lambda <- parameters::model_parameters(rc)[2,2]

# Show correction factor
  lambda

[1] 0.3920149

Finally, we can calibrate the regression coefficient of the naive analysis ($\beta\prime_{W_J=1}=$ -0.04) by dividing it by the correction factor $\lambda=$ 0.392. Once calibrated, we find that the regression coefficient should be -0.102, which is consistent with the true association!

The mecor package

Fortunately, we don’t have to calculate everything by hand. The mecor R package (Nab et al. 2021) can be used to calibrate a regression coefficient using repeated data of the independent variable measured with error. Using mecor is more efficient than the hand calculation above, as the package accommodates a wide range of scenarios and incorporates variance estimation.

The code below illustrates how to apply regression calibration with mecor. For demonstration purpose, the method=standard is used to show results consistent with traditional regression calibration, but other relevant methods can be used.

# ********************************************** #
#          Reg. calibration with mecor           #
# ********************************************** #

library(mecor)

model_mecor <- 
mecor::mecor(formula = LDL_cholesterol ~    # outcome
               MeasError(VF_day1, replicate = (VF_day2)) , # replicate measurement
             method = "standard",           # standard = regression calibration
             data = VF_simstudy)            # data

model_mecor

Call:
mecor::mecor(formula = LDL_cholesterol ~ MeasError(VF_day1, replicate = (VF_day2)), 
    data = VF_simstudy, method = "standard")

Coefficients Corrected Model:
(Intercept) cor_VF_day1 
  3.0064694  -0.1019799 

Coefficients Uncorrected Model:
(Intercept)     VF_day1 
 2.69087911 -0.03997762 

# Show confidence intervals for the corrected estimate (delta method)
  summary(model_mecor)$c$ci

             Estimate       LCI       UCI
(Intercept)  3.006469  2.890262  3.122677
cor_VF_day1 -0.101980 -0.124810 -0.079150

Upon application of the measurement error correction (via standard regression calibration), we find that the coefficient of regression for the association between vegetables and fruits and LDL cholesterol is -0.102 mmol/L per 1-serving increase in vegetables and fruits intake. This is almost exactly the true association, as per the simulation, and equal to the ‘manual’ analysis above.

Bootstrap variance estimation can also be performed within mecor with the B=... option.

Conclusion

Thanks to Nab et al. (2021), regression calibration is relatively simple to implement in R, as well as other types of measurement error correction. I must point out that dietary intake data often have other issues that were not dealt with in this simple demonstration. For example, dietary intake data are often skewed which may require transformation to satisfy the classical measurement error assumptions. Covariates were also not considered, but they would have to be included in the regression calibration model (Keogh and White 2014, Keogh et al. 2020). Also, study objectives are often much more complex; for example, many variables measured with error are often considered together in the same model. Nonetheless, I think the simple example above illustrates the importance of considering the impact of random errors and the relevance of measurement error correction methods.

For nutrition analyses in particular, I find the NCI methods currently provide the most comprehensive measurement error correction software. However, these methods are currently available in SAS only.

Reference

Djousse, L., Arnett, D. K., Coon, H., Province, M. A., Moore, L. L. & Ellison, R. C. (2004) Fruit and vegetable consumption and LDL cholesterol: the National Heart, Lung, and Blood Institute Family Heart Study. Am J Clin Nutr, 79(2), 213-7. doi:10.1093/ajcn/79.2.213.

Keogh, R. H. & White, I. R. (2014) A toolkit for measurement error correction, with a focus on nutritional epidemiology. Stat Med, 33(12), 2137-55. doi:10.1002/sim.6095.

Keogh, R. H., Shaw, P. A., Gustafson, P., Carroll, R. J., Deffner, V., Dodd, K. W., Kuchenhoff, H., Tooze, J. A., Wallace, M. P., Kipnis, V. & Freedman, L. S. (2020) STRATOS guidance document on measurement error and misclassification of variables in observational epidemiology: Part 1-Basic theory and simple methods of adjustment. Stat Med, 39(16), 2197-2231. doi:10.1002/sim.8532.

Kirkpatrick, S. I., Guenther, P. M., Subar, A. F., Krebs-Smith, S. M., Herrick, K. A., Freedman, L. S. & Dodd, K. W. (2022) Using short-term dietary intake data to address research questions related to usual dietary intake among populations and subpopulations: Assumptions, statistical techniques, and considerations. J Acad Nutr Diet, 122(7), 1246-1262. doi:10.1016/j.jand.2022.03.010.

Nab, L., van Smeden, M., Keogh, R. H. & Groenwold, R. H. H. (2021) Mecor: An R package for measurement error correction in linear regression models with a continuous outcome. Comput Methods Programs Biomed, 208, 106238. doi:10.1016/j.cmpb.2021.106238. PMID:34311414.

Thompson, F. E., Kirkpatrick, S. I., Subar, A. F., Reedy, J., Schap, T. E., Wilson, M. M. & Krebs-Smith, S. M. (2015) The National Cancer Institute’s Dietary Assessment Primer: A Resource for Diet Research. J Acad Nutr Diet, 115(12), 1986-95. doi:10.1016/j.jand.2015.08.016.